Warmachine: Those Fickle Dice


Come close math-junkies. Here are some things to bear in mind when thinking about dice probability in Warmachine/Hordes (WM/H)
Dice, Math, and You
One of the defining features of WM/H is how much dice math and probability factors into the game. For the most part, attack and damage rolls in WM/H use 2d6 to determine their outcome, with the option to add extra dice using special rules (boosting, Weaponmaster, feats, etc).
This is important because rolling summed sets of dice gives you something to base your expectations on – the probable outcome of rolling that set of dice – and you can use that inform your decisions. All of the stats and many of the special abilities in the game are based around that math, so lets take a look at some fundamentals.
Reading Is Fundamental
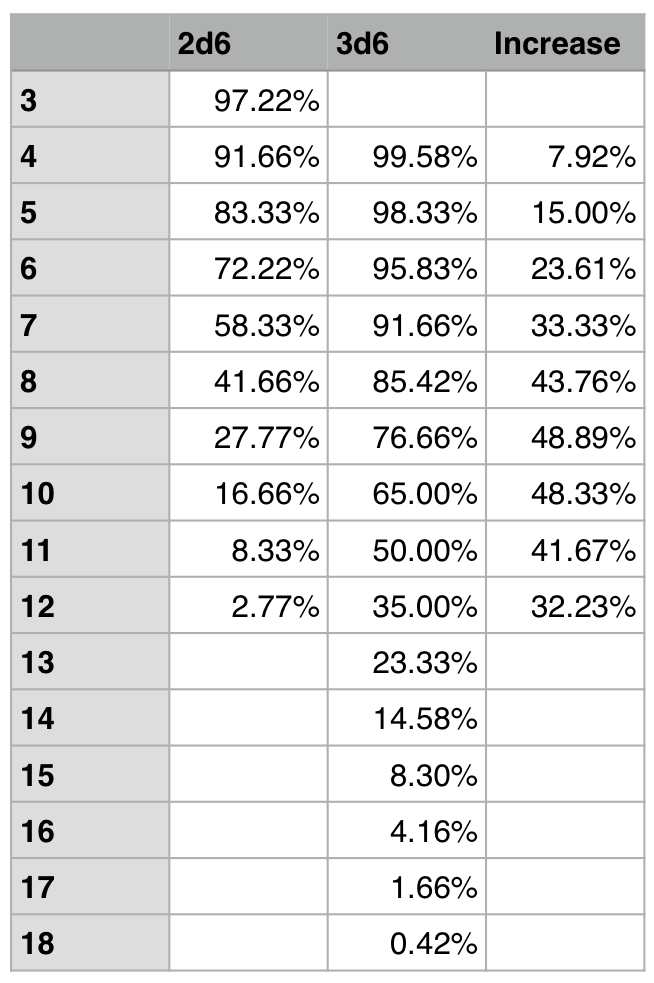
At some point in your WM/H playing time, you’ll want to get really friendly with a table like this:
An example to illustrate how to read the chart: If you have MAT 6 and are trying to hit a DEF 13 target, you need a 7+ on your resulting roll. Thus, you have a 58.33% chance to succeed when rolling 2d6, and a 90.74% chance to succeed if you’re rolling 3d6.
You don’t need to be able to recite it from memory (but that doesn’t hurt if you’ve got a head for numbers that way); the most important thing is coming away with an intuitive feel for what some key probabilities are.
To continue with the previous example: having a rough idea of the probabilities lets you know that you have around a 50/50 chance to suceed on 2d6, and a very high chance to succeed on 3d6.
Numbers to Watch
Here is a quick crib sheet of some of the probabilities I’ve found come up most often in game (for when you’re rolling 2d6 or 3d6):
- Need a 7+ to succeed – 58.33% using 2d6, 90.74% using 3d6.
- Need an 8+ to succeed – 41.67% using 2d6, 83.80% using 3d6.
- Need a 10+ to succeed – 16.67% using 2d6, 62.50% using 3d6.
- Need an 11+ to succeed – 8.33% using 2d6, 50.00% using 3d6.
These numbers come up often during games of WM/H, and they also represent important break points that can help you gauge your odds at a glance (which can help when evaluating when to boost rolls).
Needing a 7+ is the last point where rolling 2d6 yields fairly good results. After that you’re on the losing side of the exchange more often than not, and it is worth considering boosting your rolls if possible. Needing a 10+ vs needing an 11+ is when even 3d6 rolls start to get away from you. Just that one point of difference is enough to turn a roll from “decently likely” to ” coin flip” (and it only gets worse from there).
The Golden Rule
There is a very, very important thing to bear in mind whenever talking or thinking about dice probabilities. That is:
Probability only informs you of likely outcomes.
That can seem like a “duh” statement, but it is really important to bear in mind. It can be very easy to be seduced by knowing the odds of success and failure and feel like you have a handle on how things are going to play out. However, that hubris often ends up coming back to bite you. A 99% chance to succeed still brings with it a 1% chance of failure, and if you aren’t ready for that 1% you can end up in some bad places (mentally and on the tabletop).
Knowing the numbers is important to success in WM/H, but only in so much as it puts you in a good position to make informed decisions. G.I. Joe had it right.
—–
Dice can be your friend in WM/H, and they’ll just as often be your enemy. Let us all use our newfound knowledge of dice math to commiserate about terrible rolling moments in the comments below.
Also check out Sticks and Dice for more Warmachine and Hordes content!