Board Games History: Two Mathematicians Accidentally Created the Same Game


Hex combines strategy, clever tactics and has a profound mathematical underpinning related to the Brouwer fixed-point theorem.
Okay, yes. Your caught me. I pulled that directly from Wikipedia. But for as much as I love math in games and game theory, I have no idea what Brouwer fixed-point theorem is, and have no intention of looking it up. At least, not right now.
Today, we’re looking at a game called Hex.
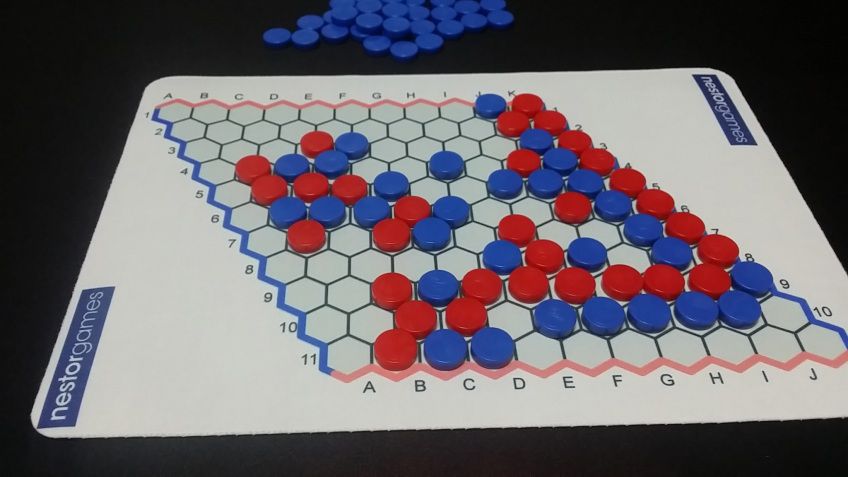
Just for some Play Along At Home, the picture above is an end state of a game of Hex. Who do you think won and why?
Here’s another end state. Is it a little more clear now?
Games of Hex are won by bisecting the board. The first player to create a route connecting opposite sides wins. That’s the whole game. So, why talk about such a simple game? Well, that’s because here at Board Games Retro, we like to talk about…
A Little Bit Of History
Credit for first designing Hex goes to Piet Hein, a Danish mathematician, inventor, designer, author and poet, who often wrote in Old Norse. His poems appeared in a daily newspaper called Politiken, which is still in digital circulation today.
Hein introduced his game, which he called Con-tac-tix, at the Niel Bohr Institute in 1942. However, when Hein published an article about his game in Politiken that December, he called the game Polygon and the name stuck.
Double However, at roughly the same time, in 1948 (I said roughly), mathematician John Nash independently invented the game at Princeton University. Nash was a well renowned mathematician whose theories are still widely used in economics and he even won a Noble Memorial Prize in 1994 in Economic Sciences.
As the game gained some popularity, Parker Brothers got their hands on it and published their copy in 1952, under the name Hex.
 They also published a version called Con-tac-tix in 1968.
They also published a version called Con-tac-tix in 1968.
At the time Nash’s version was being published in the July 1957 issue of Mathematical Games, Nash and his friends called the name either Nash or John; This second name being a fun poke at the fact the game could be played on hexagonal bathroom tiles.
Artificial Intelligence On Games
Games like this are like sweet ambrosia for computer scientists who are looking to solve games and program the perfect AI.
In 2002, the first explicit winning strategy was developed, but only for a 7×7 board. However, as computers advanced, scientists were able to completely solve up to a 9×9 board. Meaning that given any board state, assuming both players make ideal moves, the entire game can be predicted accurately.
In 11×11 Hex (the standard size), there are approximately 2.4×1056 possible legal positions. Compare this to the 4.6×1046 legal positions in chess, and it suddenly makes sense why this is taking a while to figure out.
Regardless of this, programmers are still making powerhouse AI opponents. In October of 2019, the program Mootwo won against the top ranked human player.
There are plenty of AI bots to play against, but this is the one I chose to lose to over and over to.
Final Thoughts
Brouwer’s fixed-point theorem is a fixed-point theorem in topology, named after L. E. J. (Bertus) Brouwer. It states that for any continuous function 


okay…. coolcoolcool. Yeah, totally.