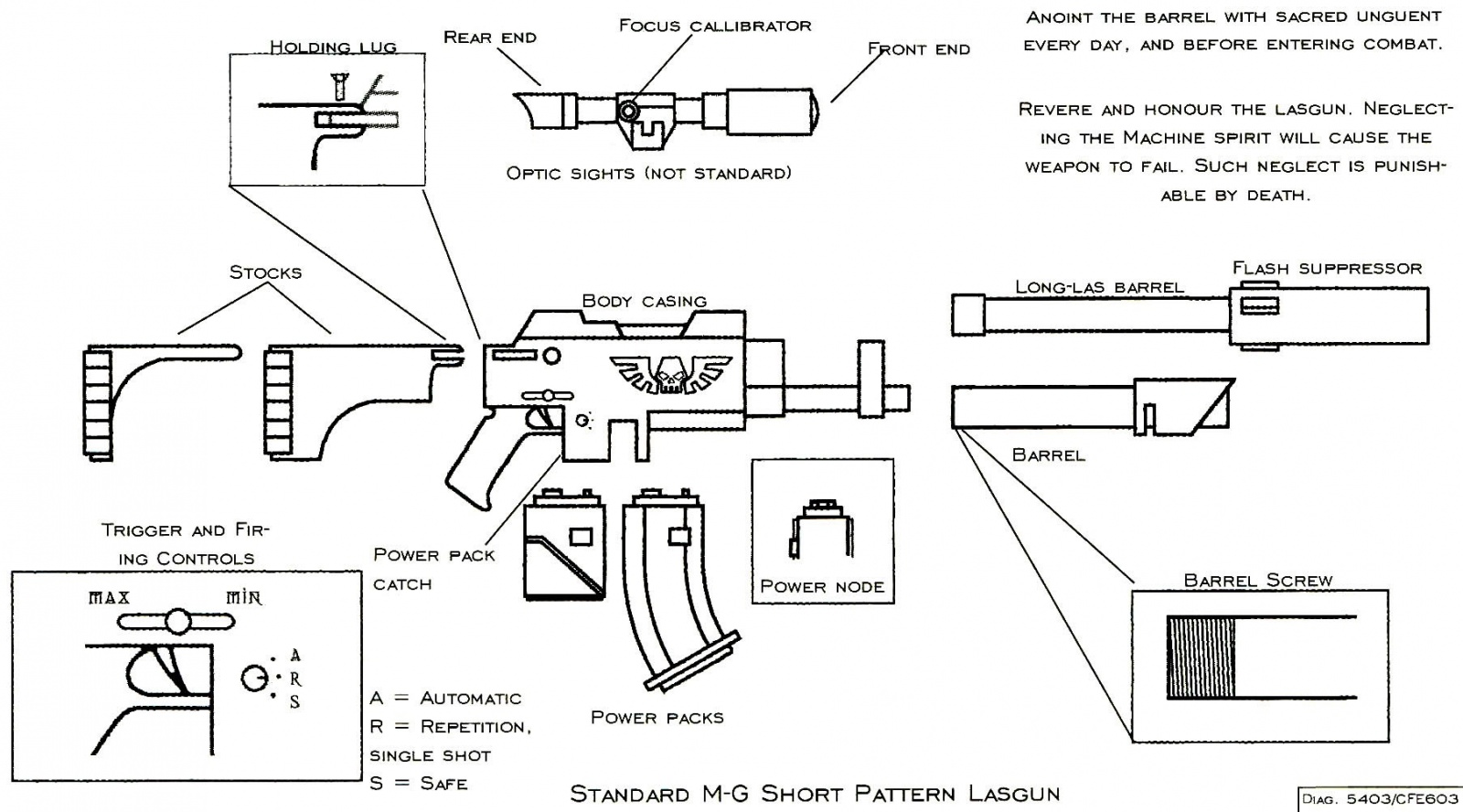
Warhammer 40K: The Fall of The Lasgun


Let’s talk about how the Lasgun has fallen out of favor as a useful weapon.
Last week I discussed the issues 9th Edition is having in regards to low quality troops. In short, the move to a huge number of basic troops now having two wounds, coupled with large percentage point increases on lower quality troops and increased damage output for elite units, such as Space Marines, has left bottom tier troops in a very rough spot. Where once large numbers allowed them to make for their poor quality this isn’t really the case anymore. Today I wanted to take a closer look at one aspect of this, the humble lasgun.
The Hero of the Imperium 
The lasgun has long been one of the worst, though not THE worst, guns in 40K. It combines low strength, ap, and damage with… well nothing else. Not for nothing is it nicknamed the flashlight, a tool that is often said to be as effective a weapon. However the lasgun has also long been a story of the success of numbers and discipline. While individually weak, they remained cheap enough that with large enough numbers, often firing in disciplined volleys, you could bring even large enemy targets. Coupled with the Astra Militarum’s orders and other rules that reward formation fighting a lasgun could become quite useful. I personally have run infantry guard hordes competitively since 3rd Edition and had a large amount of success bringing sheer numbers and weight of fire to bear. However, I fear those days are gone.
The Mixed Blessings of 8th Edition
8th Edition was the first major change for lasguns in a while. Five things, in particular, affected them:
- AP changed to a minus to armor saves. While this didn’t directly affect lasguns, as they kept AP -, it tended to make the people carrying lasguns a little more durable, letting you get off more shots.
- Cover changed. In the past it tended to give models a 5++ or 4++ save. This very rarely had any effect on Lasguns as most units used their base save. Giving a +1 save to enemy units tended to make the lasgun now worse against units in cover. In some cases however it again made the people carrying them harder to kill, though not all.
- Primaris Marines were introduced and a number of other models, in particular Terminators, increased their wounds to 2 or more. These units became highly resistant to lasgun fire, with some of them doubling their durability. However, in the early years in particular, Primaris Marines were not often taken in large numbers and the average infantry you faced was still likely to have 1 wound.
- Vehicles switched from an Armor Value to toughness and as a result, Lasguns were able to hurt them, though not easily.
- First Rank Fire! Second Rank Fire! got buffed allowing for more attacks at close range.
All in all, it was something of a mixed bag for lasguns, with some changes making them better, and few making them worse. At the end of the day for much of the edition however units armed with Lasguns remained cheap enough to be taken in numbers that were still relevant.
9th Edition and the Fall
I’ve already discussed in my last article why the units carrying lasguns, and other low-quality troops got worse in 9th. Now, let’s take a deeper look at the lasgun on its own and how it has fallen in effectiveness. In particular how it has become vastly less cost effective of a weapon.
At the end of 8th Edition to kill a basic non-Primaris MEQ model, such as a Tactical Marine, one of the more common statlines in the game you needed an average of 18 lasgun shots (netting you 9 hits, 3 wounds, and one failed save killing a model). The most effective way to get this many shots would be to have 5 Guardsmen within 12 inches of the target and buffed with the First Rank Fire! Second Rank Fire! Order. At 4 pts a model, that would cost you 20 pts of Guardsmen. In addition in order to get FRF!SRF! you needed an officer. At 30 pts and able to buff two squads (without using any bonus options) a Company Commander can be said to add 7.5 pts to our five Guardsmen. This is of course a rough number as the Commander has value beyond just buffing those models, but it’s an easy number for use. With a Tactical Marine at 12 pts it can thus be said you needed 27.5 pts of Lasgun fire (at the right range and positioning) to kill a basic Marine or 55 pts to kill a 17pt Primaris Marine. 
Let’s jump to right now. To kill that same Tactical Marine you now need not 18 lasgun shots, but 36 (netting you 18 hits, 6 wounds and 2 failed saves killing the one model). This is effectively the damage output of an entire Infantry Squad under the effects of FRS!SRF! at close range (which gets 37 shots, one extra). Thanks to point jumps that squad, and the half of a Company Commander needed to buff them will cost you 67.5 pts, while the same Tactical Marine has jumped up by 6 pts to 18 pts. (and the Primaris Marine has jumped up to 20 pts).
In short, the points needed to kill a single basic Tactical Marine changed from 27.5 in 8th Edition to 67.5 pts in 9th Edition, or a 40 pt jump, while the same Marine saw only a 6 pt increase in pts. The cost to kill the model went up about 7x the cost of the model itself. The cost to kill a Primaris model on the other hand went up a mere 12.5 pts vs a 3 pt jump for the Primaris unit, merely 4x the pts increase of the target. Should you attempt to engage these targets outside of 12 inches (where you will be safer from devastating return fire and charges, you will of course have to double the number of models needed, meaning that beyond 12″ it will cost you 135 pts of Lasgun fire to kill a single Tactical Marine.
This of course means that in order to kill a single Tactical Squad, or CSM Squad you now need to have 100 Guardsmen within 12 inches, and all benefiting from FRF/SRS (Or 3 Company Commanders, 3 Platoon Commanders and either a special charter or stratagem/trait allowing an extra command). In all this 665 pts to wipe out a base 180 pt unit, that is assuming you can get 100 Guardsmen within 12″ and unharmed to deliver that firepower. Which of course you can’t.
Final Thoughts
As you can see the effectiveness of the Lasgun has rapidly dropped with the onset of 9th Edition. Not only are the people carrying them far more vulnerable to enemy fire and assault, but the cost bumps have let you take fewer guns than you need. While this was to a degree true in 8th, due to Intercessors and other Primaris Marines, the base unit you were most likely to fight remained a 1 wound model. In 9th that is radically changed with half or more of the armies in the game, Marines and CSM (not to mention Custodes) having 2+ wound base models and more higher-wound models showing up in other armies all the time. Though units did get a bump in points to account for the extra wounds, it was a far smaller pts increase, relatively speaking, than the increase in cost to Guard, even before you take into account the need for twice as many shots. Given this massive disparity in points and firepower we are now seeing, without a major fix, after nearly 20 years I’m simply at a loss as to what good a lasgun is anymore and don’t see how to move forward with an infantry heavy Guard army. Something that saddens me greatly.
Let us know how you’d fix lasguns, down in the comments!